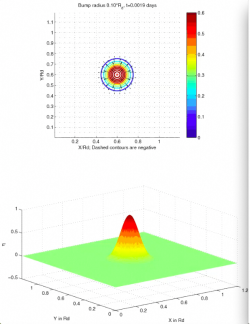
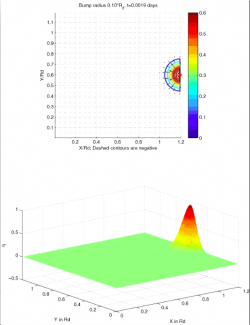
I used Francois
Primeau's linear shallow water model to model the evolution of a
motionless mound of water that is allowed to evolve either in the middle
(left picture) or eastern edge (right picture) of a closed beta-plane
basin. In class, I motivate this with an aquarium and a mound of water
generated by an inverted glass. I include both contour and 3D plots.
 |
 |
Runs are also
made on an equatorial beta-plane to illustrate how equatorial
Kelvin and Rossby waves interact. In these runs, the initial disturbance
is always in the center of the domain.
All distances are scaled by the radius of deformation Rd, defined as sqrt(gH)/f, where g can either be the full gravitational acceleration or a reduced gravity, and H the full ocean depth for the former or a layer thickness. For the equatorial runs, we use the equatorial radius of deformation sqrt(gH/beta). The background viscosity is low -- 2*dx noise dissipates in 100 days. Without further ado, here are the movies:
| Size of initial bump |
0.1Rd |
1Rd | 3Rd | 10Rd |
| Mid-latitude, center of ocean |
movie |
movie | movie | movie |
| Mid-latitude, eastern boundary |
movie | movie | movie | movie |
| Equatorial beta-plane |
movie | movie | movie | movie |
Note that the Poincare waves that mediate the Rossby adjustment tend to propagate mostly southward for the larger bumps. This is because they are nearly innertial, and cannot exist to the north (in this Northern Hemisphere ocean) where the inertial period falls below their frequency. Also note how the mid-sized bumps distort with time due to the change of Rossby speed with latitude. Lots of neat stuff to see here.
Note that there is a bug in the graphics --
negative elevations are supposed to have dashed contours, but don't
because of a matlab bug in generating postscript... sigh. To be fixed.
A more complete description of the non-linear evolution of these dynamics can be found in Early et al., 2011: The Evolution and Propagation of Quasigeostrophic Ocean Eddies*. J. Phys. Oceanogr., 41, 1535–1555. doi: http://dx.doi.org/10.1175/2011JPO4601.1 and the literature it cites. This is a fun paper and well worth reading.
Many oceanographic students have learned about waves from this excellent set of notes prepared by Dave Chapman and Paola Malanotte-Rizzoli from a course originally given by Myrl Hendershott. They have been passed from hand to hand, and xeroxed many times. You may now find them here .